11 KiB
class: animation-fade layout: true
class: impact
Криптография
без криптокупюр
One Time Pad
--
-
Что это? Схема шифрования (Cipher).
--
$ c = E(k, m) $
```
7 (H) 4 (E) 11 (L) 11 (L) 14 (O) сообщение (m)
+ 23 (X) 12 (M) 2 (C) 10 (K) 11 (L) ключ шифрования (k)
= 30 16 13 21 25 m + k
= 4 (E) 16 (Q) 13 (N) 21 (V) 25 (Z) (m + k) mod 26
E Q N V Z → шифротекст (c)
```
--
m = D(k, c)
```
4 (E) 16 (Q) 13 (N) 21 (V) 25 (Z) шифротекст (c)
- 23 (X) 12 (M) 2 (C) 10 (K) 11 (L) ключ шифрования (k)
= -19 4 11 11 14 c – k
= 7 (H) 4 (E) 11 (L) 11 (L) 14 (O) c – k (mod 26)
H E L L O → сообщение (m)
```
One Time Pad
-
Какая задача? Конфиденциальность (Confidentiality).
--
- Возможность скрыть от посторонних глаз содержимое сообщения.
--
-
Насколько он хорош в этой задаче? Идеально хорош. 🌝
--
- Обладает свойством _perfect security_.
-- - Не раскрывает ни крупицы информации об исходном сообщении.
-- - Лучшее, что есть в криптографии.
--
-
Почему же им никто не пользуется? Непрактично. 🌚
--
- Размер _ключа_ должен быть не меньше размера _сообщения_.
--
|K| \gg |M|
One Time Pad
During WWII the Soviet Union could not produce enough one-time pads ... to keep up with the enormous demand .... So, they used a number of one-time pads twice, thinking it would not compromise their system. American counter-intelligence during WWII collected all incoming and outgoing international cables. Beginning in 1946, it began an intensive effort to break into the Soviet messages with the cooperation of the British and by ... the Soviet error of using some one-time pads as two-time pads, was able, over the next 25 years, to break some 2900 messages, containing 5000 pages of the hundreds of thousands of messages that had been sent between 1941 and 1946 (when the Soviets switched to a different system).
Harvey Klehr
Symmetric ciphers
Stream ciphers
--
- Например, One Time Pad.
--
- Как решить проблему с длиной ключа?
--
-
Ответ есть! CSPRNG!
--
<img src="assets/kot_gosha.jpg" style="width: 50%;" />
Stream ciphers
CSPRNG
Криптографический генератор псевдослучайных чисел (Cryptographically secure pseudo-random number generator).
--
-
Эффективный детерминированный -- алгоритм G = (S, R).
--
- На вход подаётся seed
s \in S, S = \\{0,1\\} ^ l.
--
- В результате последовательность
r \in R, R = \\{0,1\\} ^ L.
--
l \ll L!
Stream ciphers
Схема шифрования
Имея на руках надёжный генератор случайных чисел, мы можем шифровать сообщения, гарантируя их конфиденциальность.
--
E(s, m) := G(s)[0 .. v - 1] \oplus m
--
D(s, c) := G(s)[0 .. v - 1] \oplus c
--
XOR
| 0 | 0 | 1 | 1 | = n |
|
\oplus |
0 | 1 | 0 | 1 | = m |
= |
0 | 1 | 1 | 0 |
--
| \oplus | 0 | 1 | 0 | 1 | = m |
| | 0 | 0 | 1 | 1 | = n |
Semantic security
--
Возможность скрыть абсолютно всю информацию от глаз злоумышленника не представляется возможным.
Нужна более практичная возможность измерить надёжность той или иной схемы шифрования.
--
- Злоумышленники обладают ограниченными вычислительными ресурсами.
--
- Схема шифрования надёжна, если вероятность извлечь информацию из шифротекста крайне мала.
--
- например, $ \varepsilon \leq \frac{1}{2 ^ {80}} $,
- но не $ \varepsilon \geq \frac{1}{2 ^ {30}} $
Semantic security
Вероятностный эксперимент
--
- Мы хотим, чтобы вывод генератора был неотличим от случайного набора бит.
--
- Предложим злоумышленнику сыграть в игру, где он:
- выбирает пару сообщений (
m_0, m_1 \in M), - передаёт их честному судье,
- судья выбирает случайно одно из сообщений (
b \xleftarrow{R} \\{0, 1\\}), - шифрует его при помощи случайного набора бит (
c \leftarrow m_b \oplus \\{0,1\\}^l), - и возвращает злоумышленнику;
- тот должен решить, первое или второе сообщение было зашифровано (
b^\prime \leftarrow \\{0, 1\\}).
- выбирает пару сообщений (
--
- Вероятность выбрать правильный вариант
Pr[b = b^\prime] = \frac{1}{2}.
Semantic security
Вероятностный эксперимент
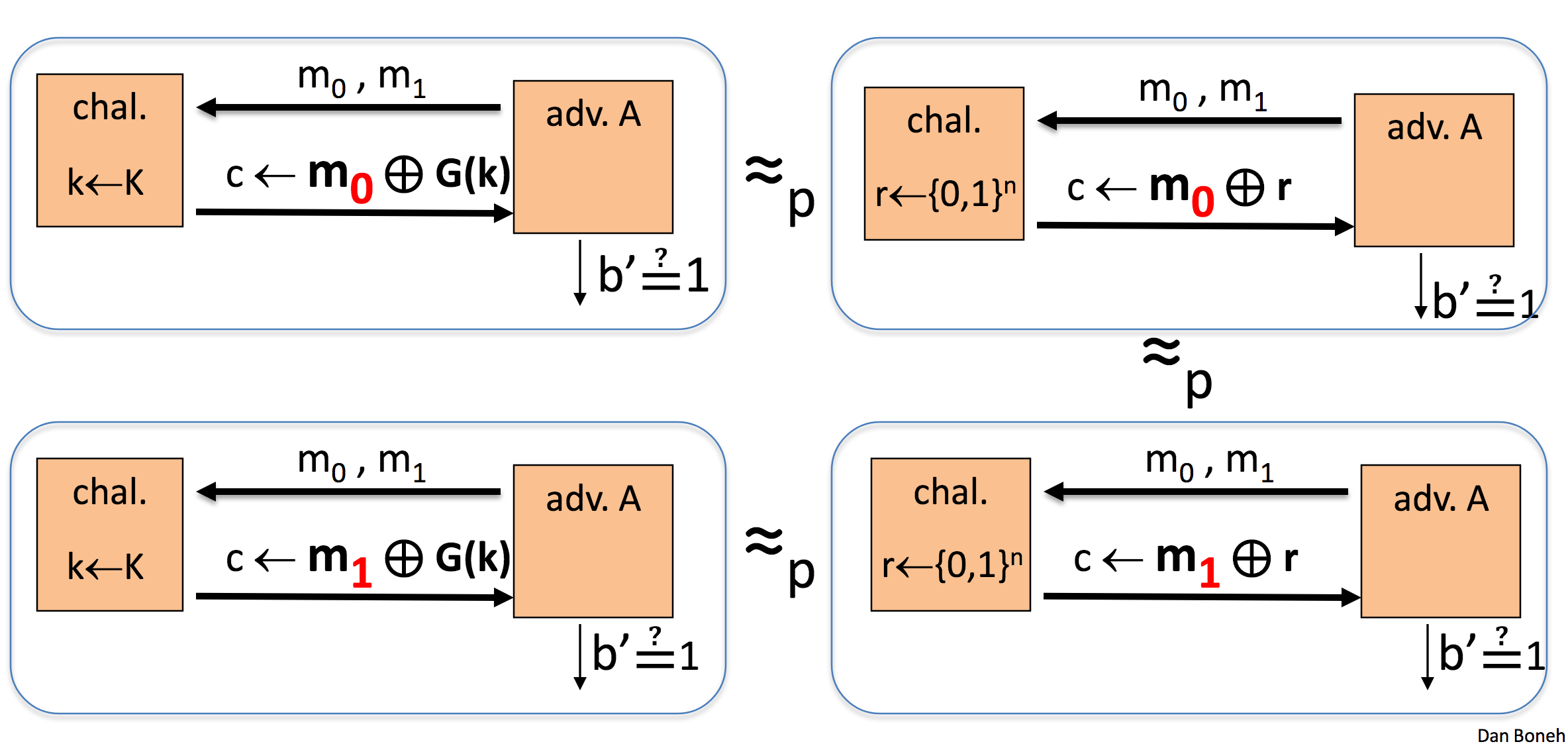
Схема надёжна, если |Pr[b_1 = b_1^\prime] - Pr[b_2 = b_2^\prime]| \leq \varepsilon.
Stream ciphers
Надёжность
-
Stream cipher семантически надёжен, если злоумышленник не может предсказать следующий бит вывода генератора случайных чисел, если ему известны все предыдущие. Но неизвестно внутреннее состояние, заданное секретным ключом. -- Генератор считается непредсказуемым (Unpredictability).
--
-
Но что если мы модифицируем игру? Дадим злоумышленнику возможность сформировать более одной пары сообщений.
--
$ c_1 \leftarrow m_1 \oplus G(k) $
$ c_2 \leftarrow m_2 \oplus G(k) $
$ m^\prime \leftarrow c_1 \oplus c_2 $
Stream ciphers
Надёжность
- Текст на естественном языке неслучаен, в
m^\primeмного информации об исходном сообщении!
--
- Если шифровать файлы, в заголовках которых часто встречается один и тот же набор бит, можно раскрыть часть вывода генератора!
--
Stream cipher нельзя использовать для шифрования различных сообщений с одним и тем же ключом!
Block ciphers
--
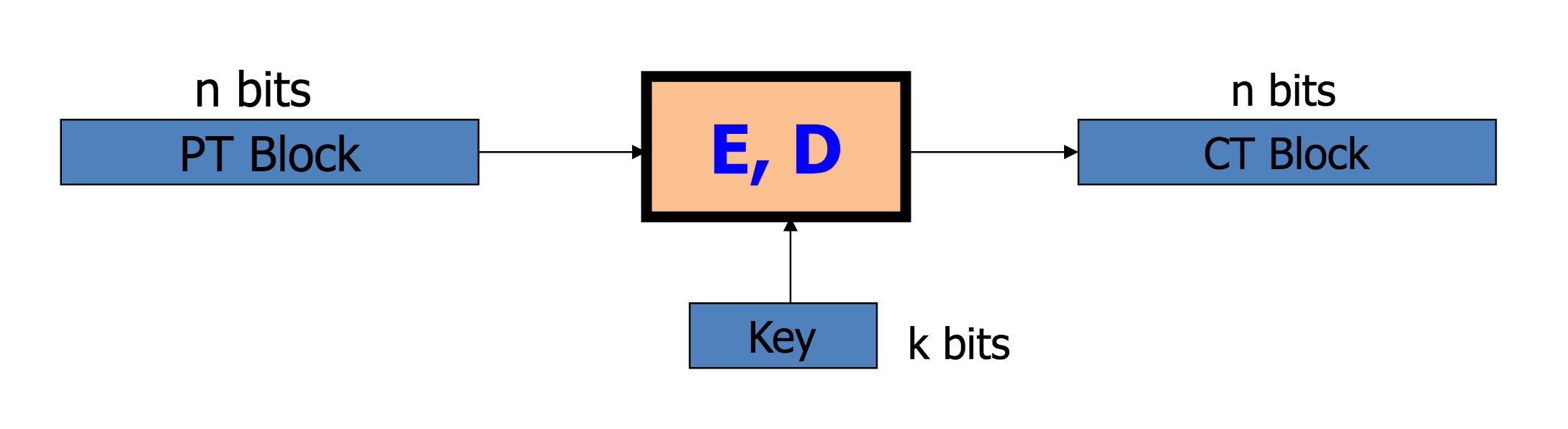
\\{ E(K, M), D(K, C) \\}
K \in \\{0,1\\}^k
M, C \in \\{0,1\\}^n
--
AES
- Блоки размера 128 бит.
- Ключ размера 128, 192 или 256 бит.
Block ciphers
Надёжность
-
Можно использовать один и тот же секретный ключ более одного раза. Устойчив к модифицированной игре со злоумышленником. -- Называется Chosen Plaintext Attack, сокращённо CPA.
--
-
Злоумышленник должен отличить схему шифрования от идеально случайной функции перестановки (Perfect Random Permutation).
k \xleftarrow{R} K, f \leftarrow E(k, \cdot) \Rightarrow |E(k, \cdot)| = |K| = 2^kf \xleftarrow{R} Perms[M] \Rightarrow |Perms[M]| = |M|! \approx 2^{2^{135}}
--
- Блоки ограниченного размера. Как зашифровать сообщение любой длины?
Block ciphers
Electronic Code Book (ECB)
Что если мы просто разобьём на блоки и зашифруем каждый блок по отдельности?

--
-
Не является семантически надёжной схемой. Блоки с одним и тем же содержимым шифруются в идентичный шифротекст. m_1 = m_2 \Rightarrow c_1 = c_2
Block ciphers
Deterministic Counter Mode (CTR)
Что если мы разобьём на блоки и будем складывать их содержимое с результатом шифрования номера блока?
m[0] |
m[1] |
... | m[l] |
|
\oplus |
E(k,0) |
E(k,1) |
... | E(k,l) |
= |
c[0] |
c[1] |
... | c[l] |
--
-
Нельзя использовать один и тот же ключ дважды. Как и в случае со stream cipher.
Block ciphers
Cipher Block Chaining (CBC)
Что если мы используем случайность для схемы шифрования?
Введём Initial Vector (IV) – блок, состоящий из случайного набор бит.
--
- IV – часть шифротекста.
--
- Схема, надёжная относительно CPA.
class: impact
Криптопауза
-
PKCS7 padding
-
AES CBC padding oracle
-
Будет пятисотить на невалидный padding в последнем блоке
-
- POST
- formdata
- ct={ciphertext}
0BE60A54AD58CDE624660AA544506937
A4208766F51D2D1947AC7E63391B6680
808F4EFEE37AB03C320A2D89279F5129
18AB43988F86EFE751001965F6C043FF